Introduction
Importance of Data Structures and Algorithms
Data structures and algorithms play a crucial role in computer science and software development. They form the foundation upon which efficient and scalable solutions are built. Understanding data structures allows us to organize and store data in a way that optimizes access and manipulation. On the other hand, algorithms provide the step-by-step instructions for solving problems and performing tasks efficiently. By mastering data structures and algorithms, developers can improve the performance of their code, reduce time complexity, and create more robust and scalable applications. Therefore, it is of utmost importance for aspiring programmers and software engineers to have a solid understanding of data structures and algorithms in order to excel in their field.
Overview of Data Structures
Data structures are essential components in computer science and software development. They provide a way to organize and store data efficiently, allowing for quick and easy access and manipulation. In this article, we will provide an overview of data structures, discussing their importance and different types. Understanding data structures is crucial for building efficient and scalable algorithms, as they can greatly impact the performance of a program. By the end of this article, you will have a solid understanding of the fundamental data structures and their applications, laying a strong foundation for further exploration in the field of data structures and algorithms.
Overview of Algorithms
In the article ‘Building a Solid Foundation in Data Structures and Algorithms’, the section ‘Overview of Algorithms’ provides a comprehensive introduction to the fundamental concepts and principles of algorithms. This section aims to familiarize readers with the importance of algorithms in problem-solving and the role they play in computer science. It covers various types of algorithms, such as searching, sorting, and graph algorithms, highlighting their applications and efficiency. By understanding the overview of algorithms, readers will gain a solid understanding of the key components that form the basis of efficient problem-solving in the field of data structures and algorithms.
Arrays

Definition and Properties of Arrays
Arrays are a fundamental data structure in computer science. They consist of a collection of elements, each identified by an index or a key. The elements in an array are stored in contiguous memory locations, allowing for efficient access and manipulation. Arrays have several important properties, including a fixed size, random access to elements, and the ability to store elements of the same data type. These properties make arrays a versatile and powerful tool for organizing and manipulating data.
Array Operations
Array operations are essential in data structures and algorithms. They allow us to manipulate and access elements in an array efficiently. Common array operations include inserting an element at a specific position, deleting an element from a given position, and searching for an element in the array. These operations are the building blocks for more complex algorithms and are crucial in optimizing performance. By understanding and mastering array operations, we can lay a solid foundation for solving a wide range of problems in the field of data structures and algorithms.
Common Array Algorithms
In the field of computer science, data structures and algorithms play a crucial role in solving complex problems efficiently. When it comes to working with arrays, there are several common algorithms that every programmer should be familiar with. These algorithms provide efficient ways to manipulate and analyze array data, allowing for faster and more optimized solutions. Some of the most common array algorithms include searching for an element, sorting the array, finding the maximum or minimum element, and reversing the array. By understanding and implementing these algorithms, programmers can build a solid foundation in data structures and algorithms, enabling them to tackle a wide range of problems with confidence.
Linked Lists

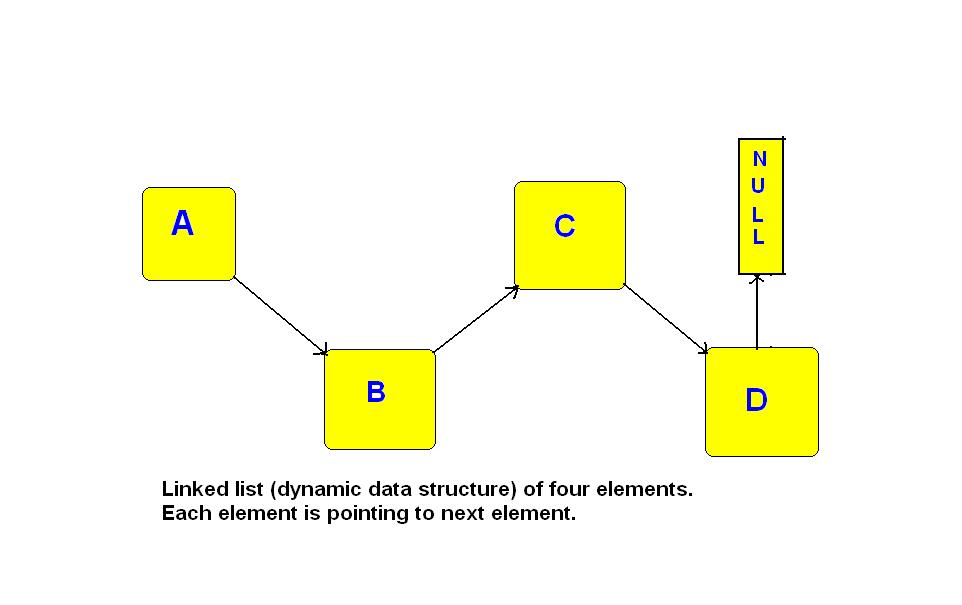
Definition and Properties of Linked Lists
A linked list is a linear data structure that consists of a sequence of nodes, where each node contains a data element and a reference to the next node in the sequence. Unlike arrays, linked lists do not have a fixed size and can dynamically grow or shrink as elements are added or removed. Linked lists are particularly useful when it comes to efficient insertion and deletion of elements, as they allow for constant time complexity. Additionally, linked lists can be easily traversed in both forward and backward directions, making them versatile for various applications in computer science and programming.
Linked List Operations
In the world of data structures, a linked list is a fundamental concept. It is a collection of nodes, where each node contains a data element and a reference to the next node. Linked lists are widely used in various applications and algorithms due to their flexibility and efficiency. In this section, we will explore the operations that can be performed on a linked list, such as insertion, deletion, and traversal. Understanding these operations is crucial for building a solid foundation in data structures and algorithms.
Common Linked List Algorithms
Linked lists are a fundamental data structure in computer science. They consist of a series of nodes, where each node contains a value and a reference to the next node in the list. Common linked list algorithms are essential for manipulating and traversing linked lists efficiently. Some of these algorithms include inserting a node at the beginning or end of the list, deleting a node, searching for a specific value, and reversing the list. Understanding and implementing these algorithms is crucial for building a solid foundation in data structures and algorithms.
Stacks and Queues

Definition and Properties of Stacks
A stack is a linear data structure that follows the Last-In-First-Out (LIFO) principle. It consists of a collection of elements where the insertion and deletion of elements can only be performed at one end, called the top of the stack. The element that is inserted last is the first one to be removed. Stacks have two main operations: push, which adds an element to the top of the stack, and pop, which removes the top element from the stack. Additionally, stacks support a third operation called peek, which returns the value of the top element without removing it. Stacks are commonly used in various applications, such as function call stacks, expression evaluation, and undo operations in text editors. Understanding the definition and properties of stacks is essential for building a solid foundation in data structures and algorithms.
Stack Operations
In the realm of data structures and algorithms, stack operations play a vital role. A stack is a linear data structure that follows the Last-In-First-Out (LIFO) principle, where the last element added to the stack is the first one to be removed. Stack operations include push, pop, and peek. Push adds an element to the top of the stack, pop removes the topmost element, and peek retrieves the topmost element without removing it. These operations are essential for managing and manipulating data in various applications, such as expression evaluation, function call management, and undo-redo functionality.
Common Stack Algorithms
In the field of computer science, data structures and algorithms play a crucial role in solving complex problems efficiently. One commonly used data structure is the stack, which follows the Last-In-First-Out (LIFO) principle. Stack algorithms are essential in various applications, including expression evaluation, function call tracking, and backtracking. These algorithms involve operations such as push, pop, and peek, allowing for efficient manipulation of the stack. By understanding and implementing common stack algorithms, developers can enhance their problem-solving skills and optimize their code for better performance.
Trees

Definition and Properties of Trees
In the context of computer science, a tree is a widely used data structure that represents a hierarchical structure. It consists of nodes connected by edges, where each node can have zero or more child nodes. The topmost node of the tree is called the root, and each node can have at most one parent node. Trees have various properties that make them suitable for solving a wide range of problems. They are efficient for storing and retrieving data, as well as for performing operations such as searching, insertion, and deletion. Additionally, trees can be used to represent hierarchical relationships, such as file systems, organization charts, and family trees.
Tree Traversal
Tree traversal is an essential concept in data structures and algorithms. It involves visiting each node in a tree data structure exactly once, following a specific order. There are different traversal techniques, such as depth-first traversal and breadth-first traversal. Depth-first traversal explores the depth of a tree before visiting its siblings, while breadth-first traversal explores the tree level by level. These techniques are crucial for understanding the structure and behavior of trees, and they play a vital role in solving various problems efficiently. By mastering tree traversal, developers can enhance their problem-solving skills and optimize their algorithms.
Common Tree Algorithms
Common tree algorithms are essential tools for solving various problems in computer science. These algorithms involve manipulating and traversing tree structures to perform tasks such as searching for a specific node, inserting or deleting nodes, and determining the height or depth of a tree. Some commonly used tree algorithms include depth-first search (DFS), breadth-first search (BFS), and binary search tree (BST) operations. Understanding and implementing these algorithms is crucial for building a solid foundation in data structures and algorithms.
Sorting and Searching

Sorting Algorithms
Sorting algorithms are an essential part of any programmer’s toolkit. They allow us to organize and arrange data in a specific order, making it easier to search, analyze, and manipulate. There are various sorting algorithms available, each with its own strengths and weaknesses. Some of the commonly used sorting algorithms include bubble sort, insertion sort, selection sort, merge sort, quicksort, and heapsort. Each algorithm follows a different approach to sorting, such as comparing and swapping elements or dividing the data into smaller subproblems. Understanding and implementing these sorting algorithms is crucial for efficient data processing and problem-solving in the field of computer science.
Searching Algorithms
Searching algorithms are an essential component of data structures and algorithms. They provide efficient ways to locate specific elements within a collection of data. There are various searching algorithms, each with its own advantages and disadvantages. Some commonly used searching algorithms include linear search, binary search, and hash-based search. Linear search is a simple algorithm that sequentially checks each element in a list until a match is found. Binary search, on the other hand, is a more efficient algorithm that works on sorted lists by repeatedly dividing the search space in half. Hash-based search algorithms use a hash function to map keys to indices, allowing for constant-time retrieval of elements. Understanding and implementing these searching algorithms is crucial for building robust and efficient data structures and algorithms.
Time Complexity Analysis
In the field of computer science, time complexity analysis is a crucial concept when it comes to designing efficient algorithms. It involves analyzing the amount of time an algorithm takes to run as a function of the input size. By understanding the time complexity of an algorithm, we can make informed decisions about which algorithm to use in different scenarios. This knowledge is particularly important in the context of data structures and algorithms, as it allows us to evaluate the efficiency and scalability of our solutions. By carefully considering the time complexity of our algorithms, we can build a solid foundation in data structures and algorithms that will enable us to solve complex problems with optimal performance.